Полиспаст — система подвижных и неподвижных блоков, соединенных гибкой связью (канатом или цепью), применяемая для увеличения силы — силовой полиспаст или скорости — скоростной полиспаст. В полиспаст входят подвижные блоки, ось которых перемещается в пространстве, и неподвижные блоки.
На рисунке 1 (позиция а) показан неподвижный блок, вращающийся по часовой стрелке под действием силы Sсбег, преодолевающей силу Sнаб. Вращение блока возможно только в том случае, если Sсбег>Sнаб, причем разность Sсбег — Sнаб достаточна для преодоления сопротивления сил трения в опоре блока и сопротивления жесткости каната или цепи при их сгибании и разгибании.
Блоки полиспаста
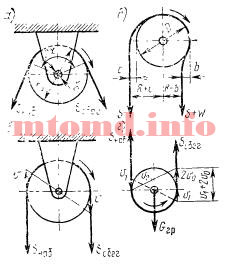
Рис. 1: а — блок с подвижной осью; б — схема набегания каната на блок; в — скорость каната на неподвижном блоке; г — скорость каната на подвижном блоке
Так как канаты, применяемые в грузоподъемных машинах, не являются абсолютно гибкими телами, а обладают определенной жесткостью, то набегающая ветвь каната не сразу ложится на ручей блока, а сбегающая ветвь не сразу выпрямляется (рис. 1, б). Жесткость каната зависит от его диаметра, конструкции, числа проволок в прядях и от числа прядей, от типа и конструкции сердечника, от механических свойств материала проволок и от трения между отдельными проволоками и между прядями. Жесткость цепи определяется в основном сопротивлением сил трения в шарнирах пластинчатой цепи или сил трения между звеньями сварной цепи.
Расчет полиспаста
Для сгибания и разгибания каната к его сбегающей ветви необходимо приложить дополнительную силу W, которая зависит от размеров и конструкции каната и блока, а также от натяжения каната. Ее можно определить из уравнения моментов сил относительно оси блока без учета сил трения в опоре блока:
![]()
где R = D/2 — радиус ручья блока; q — коэффициент жесткости (его значение определяют экспериментально). Уравнение моментов всех действующих сил относительно оси блока (рис. 1, а) имеет вид:
![]()
где N — нагрузка на ось блока, равная геометрической сумме сил Sнаб и Sсбег; do — диаметр оси блока; f — коэффициент трения в опоре блока.
При определении величины N с некоторым допущением можно принять Sнаб≈Sсбег и тогда при угле обхвата блока канатом 2α:
![]()
Подставив это соотношение в выше приведенное уравнение моментов, получим:
![]()
КПД блока
Коэффициент полезного действия блока (КПД блока) — это отношение полезной работы Sнабh при подъеме груза весом Gгр на высоту h к полной работе, совершенной при этом силой Sсбег на том же пути h с учетом преодоления потерь на трение и жесткости каната.
КПД неподвижного блока
Поэтому для неподвижного блока, у которого перемещение набегающей и сбегающей ветвей каната одинаково, КПД неподвижного блока выражается формулой:

Анализ этой формулы показывает, что чем больше угол обхвата блока канатом и чем больше жесткость каната и трение в опоре блока, тем меньше значение КПД блока и тем больше дополнительная сила, которую необходимо приложить к канату, чтобы обеспечить равномерное движение груза. На КПД блока наиболее существенное влияние оказывают потери на трение в опоре блока, зависящие от конструкции и состояния опоры, поэтому при практических расчетах с достаточной степенью точности КПД блока принимают независящим от диаметра и конструкции каната, от размеров блока и от угла обхвата его канатом. Для блоков с опорой на подшипниках скольжения η = 0,95÷0,96; для блоков на подшипниках качения η = 0,97÷0,98. Меньшие значения принимают для блоков, работающих при повышенной температуре или в запыленной или загазованной среде. Тогда натяжение ветви тягового органа, набегающей на блок:
![]()
При обегании канатом неподвижного блока скорости движения набегающей и сбегающей ветви равны между собой (рис. 1, в). Если же набегающая ветвь каната со скоростью υ1 (рис. 1, г) набегает на подвижный блок, ось которого перемещается со скоростью υо, то скорость сбегающей ветви каната равна υ1 + 2υо.
Силовой полиспаст

Рис. 2
Развернутая схема обегания канатом блоков одинарного (простого) силового полиспаста приведена на рисунке 2. Если пренебречь сопротивлением в полиспасте, то есть когда система является неподвижной, сила в любой точке каната полиспаста:
![]()
где Gгр — вес груза; a — число перерезов каната, на которых подвешен груз (в сечении К-К на рис. 2); для одинарного полиспаста это число называется кратность полиспаста.
При подъеме или опускании груза, если учитывать силы сопротивления от жесткости каната и от трения в опорах блоков, натяжение отдельных ветвей каната различно. Обозначим через S1 натяжение ветви каната, идущей на обводной блок А1, S2 — натяжение следующей ветви и т. д. В общем случае при кратности полиспаста а натяжение последней неподвижно закрепленной ветви каната равно Sа. Отсюда следует равенство:
![]()
Если ветви каната в полиспасте расположены под углом к направлению силы тяжести, то надо брать проекции сил натяжения на вертикальную ось.
Соотношение между натяжениями отдельных ветвей каната при подъеме груза:
![]()
где η — КПД блока.
Используя эти соотношения, получаем:
![]()
Вычислив сумму геометрической прогрессии (выражение в скобках), определим соотношение между весом груза Gгр и натяжением каната S1 при параллельном расположении ветвей полиспаста без учета динамических нагрузок:
![]()
Натяжение Sбар каната, подводимого к барабану Б (рис. 2), больше натяжения S1, поскольку необходимо преодолевать сопротивление в обводных блоках А1, А2, А3. Если число обводных блоков равно t, максимальное натяжение каната при подъеме груза:
![]()
При опускании груза максимальное натяжение Sа будет в последней ветви, оно равно:
![]()
КПД полиспаста
КПД полиспаста, имеющего кратность а, в целом определяется как отношение полезной работы при подъеме груза Gгр на высоту h к затраченной при этом работе Sбарah, то есть:
![]()
При этом максимальное натяжение в системе полиспаста при подъеме груза может быть определено по зависимости:
![]()
КПД подвижного блока
Подвижный блок, который следует рассматривать как полиспаст с кратностью а = 2, согласно формуле КПД полиспаста будет иметь КПД ηподв = (1 + η)/2, то есть несколько превышающий значение КПД неподвижного блока.
